Como Comprender las fórmulas matrices básicas
¿Has oído hablar de las misteriosas “fórmulas matrices”? ¿Los usas? ¿O es usted como la mayoría de los usuarios de Excel? Los ha colocado en la pila de "demasiado difíciles" y nunca más los volverá a ver. Siempre parecen surgir en los foros como soluciones a algunas preguntas complicadas sobre fórmulas.
En esta publicación, quiero presentarles un tipo de fórmula matricial que en realidad es bastante fácil de entender y se puede aplicar a muchas situaciones de la vida real. Una vez que haya comprendido el concepto de este tipo de fórmula matricial, podrá aplicarlo una y otra vez. Tus compañeros de trabajo te mirarán como si fueras un genio de Excel y quedarán hipnotizados por el cálculo aparentemente imposible que acabas de realizar. . . pero en secreto sabrás que no fue tan difícil.
Conceptos básicos de la fórmula matricial
Una fórmula matricial es un cálculo que funciona con una matriz o serie de datos. No te preocupes si ese concepto te deja boquiabierto en este momento; al final de esta publicación, con suerte, tendrá sentido.
A menudo, las fórmulas matriciales se ingresan presionando Ctrl + Shift + Enter, de ahí que a veces se las denomine fórmulas CSE. Hay funciones de matriz que no requieren el uso de Ctrl + Shift + Enter. Por lo tanto, tenga en cuenta que Ctrl + Shift + Enter no se aplica a todas las fórmulas matriciales.
El tipo de fórmula matricial que usaremos en este ejemplo requiere Ctrl + Shift + Enter. Una vez que se haya ingresado la fórmula en la barra de fórmulas, no solo presione Enter, sino presione Ctrl + Shift + Enter al mismo tiempo. Sabrá cuándo ha funcionado porque Excel mostrará automáticamente un "{" (llave de apertura) al comienzo de la fórmula y un "}" (llave de cierre) al final de la fórmula.
Debe presionar Ctrl + Shift + Enter, no solo cuando crea la fórmula por primera vez, sino cada vez que la edita.
En los ejemplos siguientes mostraré las llaves { }, pero recuerde, no las escriba, Excel las mostrará por sí solo.
Ejemplo de fórmula matricial básica
Para nuestro ejemplo, veremos el tipo de fórmula matricial que devuelve el resultado en una sola celda.
Vamos a recrear la función SUMAR.SI como una fórmula matricial. ¿Por qué? Esperemos que ya comprendas la función SUMAR.SI, así los conceptos serán más fáciles de entender. El objetivo no es recrear un SUMIF usando una fórmula matricial, sino aprender los conceptos para que puedas aplicarlos a tus propios escenarios.
Mire la tabla de datos a continuación, muestra las ventas trimestrales de 3 departamentos de una tienda de ropa. Si quisiéramos saber el total anual de cualquier departamento podríamos utilizar la función SUMAR.SI.
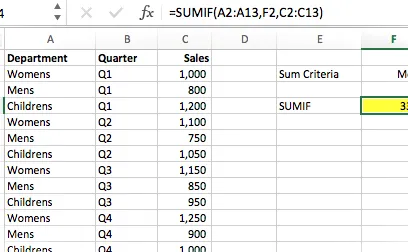
El valor de la celda F4 calcula las ventas totales del departamento de ropa masculina:
=SUMAR.SI(A2:A13,F2,C2:C13)
Dividamos la función SUMAR.SI en sus dos partes SUMA y SI. La lógica requiere que primero se calcule la función SI, luego se puede usar la función SUMA para calcular el total. Esto es lo que haremos.
El primer paso para convertir SUMAR.SI en una fórmula matricial es crear una función SI para una sola fila.
=SI(A2=F2,C2,0)
El segundo paso es expandir el rango para incluir todas las celdas requeridas para el cálculo (esto es lo que hace que esta sea una fórmula matricial, ya que calcula en función de una matriz de celdas).
=SI(A2:A13=F2,C2:C13,0)
El tercer paso es incluir la función SUMA alrededor de la función SI.
=SUMA(SI(A2:A13=F2,C2:C13,0))
El último paso es presionar Ctrl + Shift + Enter para ingresar la fórmula (observe que Excel muestra {} solo).
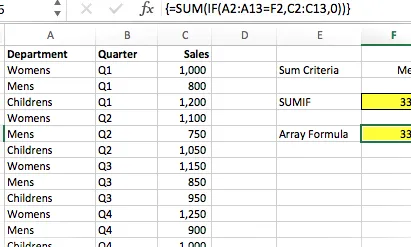
La fórmula en la celda F6 es:
{=SUMA(SI(A2:A13=F2,C2:C13,0))}
Acaba de crear una fórmula matricial. Eso no fue tan difícil, ¿verdad?
Entendiendo el cálculo
Entendamos brevemente por qué funciona esta fórmula.
{=SUMA(SI(A2:A13=F2,C2:C13,0))}
La sección de la fórmula en azul arriba se calculará como VERDADERO o FALSO para cada celda. Hace A2 = F2, luego A3 = F2, luego A4 = F2, y así sucesivamente. Como F2 es una sola celda, esto se utiliza como comparación para cada celda de A2 – A13.
Hay 12 celdas en el rango, por lo que hay 12 resultados VERDADERO/FALSO.
{=SUM(SI({FALSO;VERDADERO;FALSO;FALSO;VERDADERO;FALSO;FALSO;VERDADERO;FALSO;FALSO;VERDADERO;FALSO},C2:C13,0))}
La sección naranja en la fórmula anterior se calculará como se muestra a continuación.
{=SUM(SI({FALSO;VERDADERO;FALSO;FALSO;VERDADERO;FALSO;FALSO;VERDADERO;FALSO;FALSO;VERDADERO;FALSO},{1000;800;1200;1100;750;1050;1150;850;950 ;1250;900;1000},0))}
Cada uno de los resultados de estas fórmulas se calcula como una función SI separada.
{=SUM(SI({FALSO;VERDADERO;FALSO;FALSO;VERDADERO;FALSO;FALSO;VERDADERO;FALSO;FALSO;VERDADERO;FALSO},{1000;800;1200;1100;750;1050;1150;850;950 ;1250;900;1000},0))}
La primera función SI se ha calculado como FALSA, por lo tanto el resultado será cero (habría sido 1000, si fuera VERDADERO)
{=SUM(SI({FALSO;VERDADERO;FALSO;FALSO;VERDADERO;FALSO;FALSO;VERDADERO;FALSO;FALSO;VERDADERO;FALSO},{1000;800;1200;1100;750;1050;1150;850;950 ;1250;900;1000},0))}
La segunda función SI se ha calculado como VERDADERA, por lo tanto el resultado será 800 (hubiera sido cero si fuera FALSO)
Esto continúa para cada resultado de la función SI. Esto se calcula para proporcionar el siguiente resultado.
{=SUM({0;800;0;0;750;0;0;850;0;0;900;0}))}
Esta es ahora una función SUMA sencilla, que sumará los números. El resultado es 3300 (que es exactamente lo mismo que SUMAR.SI).
Aplicando el concepto de fórmula matricial
Este concepto funciona para una variedad de situaciones. Ahora que conoces el concepto, puedes crear tus propias fórmulas complejas, lo que sería imposible con una función normal.
Podrías crear una función SUMIFBUTFIXEDVALUEIFNOT (Suma si, pero valor fijo si no):
{=SUMA(SI(A2:A13=F2,C2:C13,500))}
O tal vez la función PROMEDIOOWNUMBER (número de fila promedio):
=PROMEDIO(FILA(A2:A13))
También puede crear el beneficio de columnas auxiliares sin necesidad de crear una columna auxiliar. En el siguiente ejemplo, las celdas E14 F14 se combinan en un único criterio de búsqueda y luego se comparan con A2 B2 combinadas, luego con A3 B3 combinadas, luego con A4 B4 combinadas, y así sucesivamente.
=COINCIDIR(E14F14,A2:A13B2:B13,0)
Advertencias
Las fórmulas de matriz pueden parecer geniales, pero hay algunas cuestiones que se deben tener en cuenta:
- Pueden ser muy lentos de calcular y, a menudo, son mucho más lentos que usar una columna auxiliar.
- La mayoría de la gente no entenderá tu trabajo (aunque esto puede ser algo bueno)
- Si no se utiliza Ctrl + Shift + Enter, es probable que se muestre #VALOR o, peor aún, un resultado incorrecto.
Otros ejemplos de fórmulas matriciales
Aquí hay algunas publicaciones del blog que incluyen otros ejemplos de fórmulas matriciales.
- Crea un Top 10 usando fórmulas
- BUSCARV: enumera todos los elementos coincidentes
- BUSCARV: busque el enésimo elemento (sin columnas auxiliares)
- BUSCARV con múltiples criterios
- Cómo la BUSCARV a la izquierda

Deja una respuesta